Fortbildungsangebote im Fach Mathematik

Die Unterrichtsmaterialien des MINT-Lernzentrums zeichnen sich durch die sorgfältige Umsetzung von Lernformen aus, die sich in empirischen Vergleichsstudien als besonders lernwirksam erwiesen haben. Dazu zählen Unterrichtseinstiege, bei denen die Lernenden schrittweise angeleitet werden, mathematische Konzepte wie zum Beispiel das Konzept der Steigung durch Vergleiche und Kontrastierungen selber zu konstruieren (Inventing with Contrasting Cases).

Wir bieten auch Fortbildungen für Fachschaften an. Mehr dazu hier

Download Programmübersicht Mathematik (PDF, 76 KB)

Beispielaufgabe: Erfinden Sie eine Masszahl für "Steilheit".

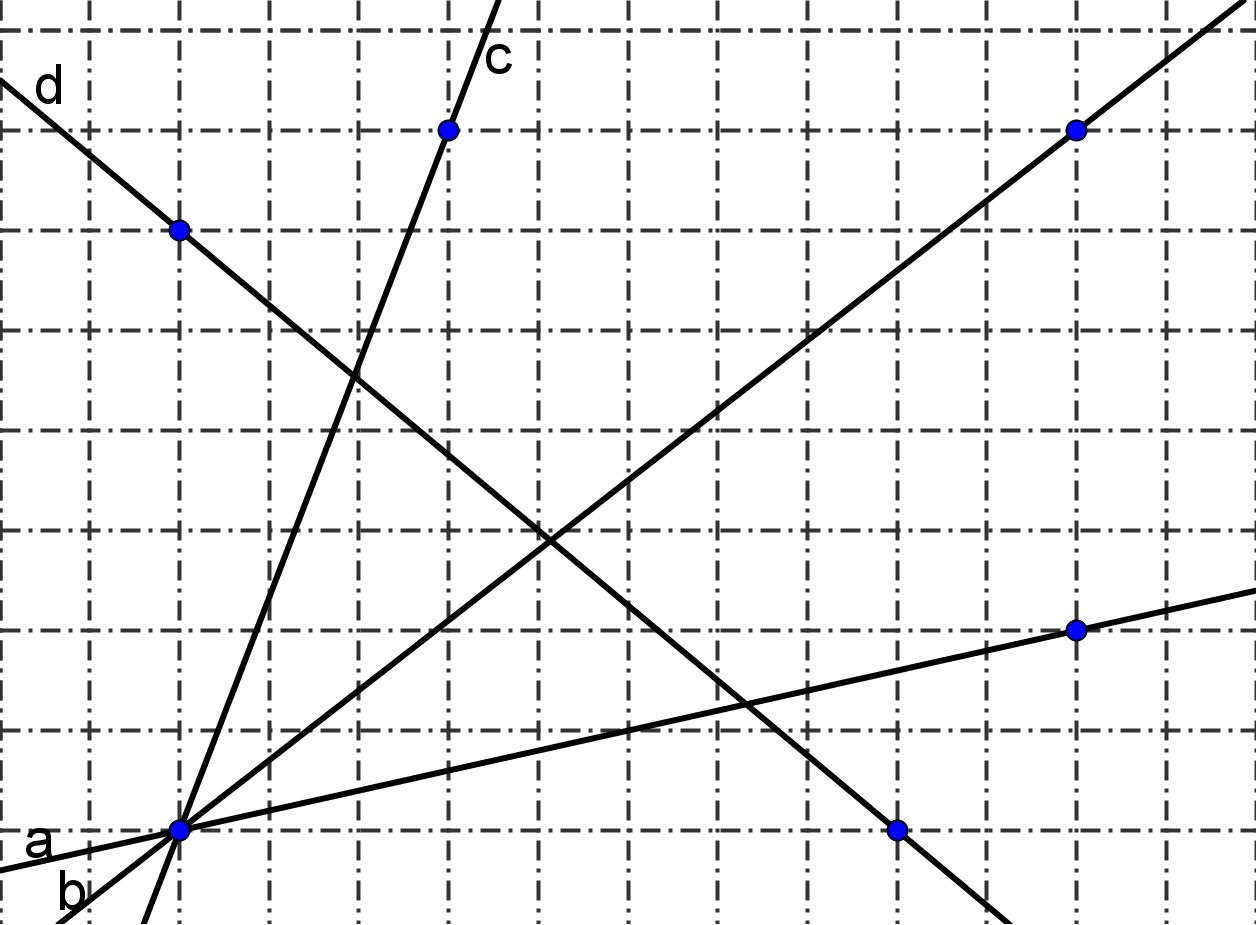
Ein weiteres kognitiv aktivierendes Vorgehen beim Einstieg in neue Themen besteht darin, bei den Lernenden zunächst das Interesse zu wecken, indem man sie durch geeignete Aufgaben auf die Grenzen ihres bisherigen Wissens aufmerksam macht. Solche Unterrichtseinstiege aktivieren zudem ihr Vorwissen und bringen sie dazu, intensiv über die mathematische Problemstellung nachzudenken. Ein Beispiel ist der folgende Auftrag zu quadratischen Gleichungen, bei dem die Schülerinnen und Schüler angeleitet werden, das quadratische Ergänzen selber zu entdecken.

Beispielaufgabe: Eifern Sie Al-Chwarizmi nach!

Abu Dscha’far Muhammed ibn Musa al-Chwarizmi war ein arabischer Mathematiker und Universalgelehrter, der den grössten Teil seines Lebens in Bagdad verbrachte, wo er im „Haus der Weisheit“ tätig war, einer Art wissenschaft- licher Akademie, die im Jahr 825 n. Chr. gegründet worden war. Die Art und Weise, wie wir heute quadratische Gleichungen lösen, geht auf ihn zurück. Sie haben hier die Gelegenheit, dem grossen arabischen Mathematiker nachzueifern, indem Sie seine Methode selbständig entdecken. Betrachten Sie dazu die quadratische Gleichung x²+ 6x=40

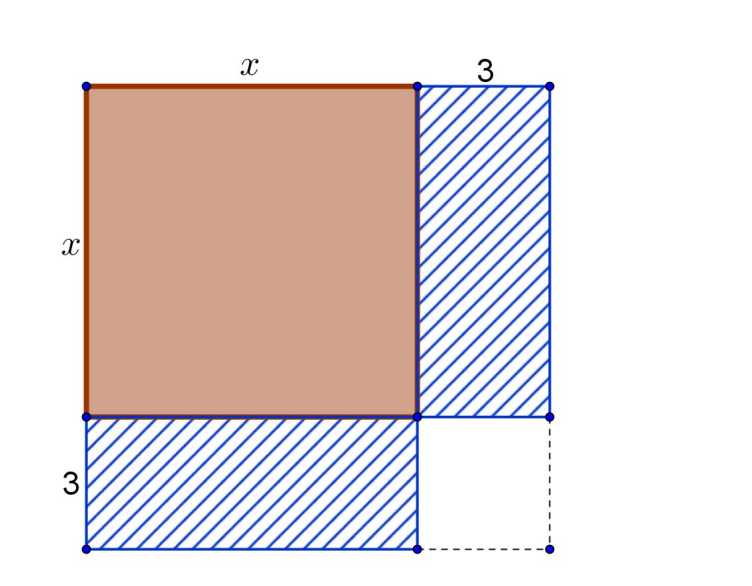
Sie könnten den Term x² geometrisch als Quadrat mit Seitenlänge x interpretieren, jedenfalls für den Fall x > 0 . Den Summanden 6x=2· 3x könnten Sie analog als zwei kongruente Rechtecke auffassen, von denen jedes die Seitenlängen 3 und x hat:

Was fällt nun auf?

Wenn man zu x²+ 6x die Zahl ... addiert, entsteht ein neues Quadrat, nämlich das Quadrat mit der Seitenlänge ... . Welche neue Gleichung entsteht also? Und können Sie diese nun lösen? Und woran genau liegt das?

Zur Vertiefung des Gelernten werden zu allen Lektionen umfangreiche Aufgabensammlungen angeboten, zu denen auch so genannte Selbsterklärungs-Aufträge gehören, die die Lernenden dazu bringen sollen, über besonders wichtige Konzepte sowie über gängige Fehlvorstellungen noch einmal nachzudenken.

Beispielaufgabe

Max soll die Gleichung x² + c= 0 lösen, in der c eine reelle Zahl ist. Er argumentiert so: „Die Zahl x² ist schon mal sicher grösser oder gleich 0. Wenn man dazu noch eine weitere Zahl addiert, kann man nie im Leben bei 0 landen. Die Gleichung besitzt also sicherlich keine Lösung.“ Erklären Sie Max, was an diesem Argument falsch ist und worauf er folglich gut achten muss.

Unterrichtssequenzen - zwei Videobeispiele

Hier sehen Sie exemplarisch, wie Armin Barth neue Konzepte einführt und erklärt. Während das erste Video die Umkehrfunktion thematisiert, widmet sich das zweite Video der Kettenregel.