Beschreibende Statistik
- Nächster Termin: nach Absprache
- Kursleitung: Lorenz Stäheli
- Autor: Lorenz Stäheli
- Schulstufe: 10. – 12. Schuljahr, Gymnasium
- Umfang: 16 Lektionen
- Kosten: 600 CHF
Anmeldung über diesen externe Seite LINK
Anregende Unterrichtseinstiege zur Vorbereitung auf das Lernen
Am Anfang des Lernens steht die Einsicht, dass man etwas noch nicht weiss. Um die Schülerinnen und Schüler auf ein neues Thema vorzubereiten, sollte ihnen daher zunächst bewusstgemacht werden, dass ihnen ein bestimmtes Wissen fehlt. Ausserdem sollen sie die Gelegenheit haben, relevantes Vorwissen zu aktivieren.
Wie lässt sich die Standardabweichung einführen?
Beim produktiven Scheitern befassen sich die Schülerinnen und Schüler mit einem Problem, welches sie wahrscheinlich nicht lösen können. Bei der Bearbeitung setzen sie sich aber mit der Problemstellung auseinander, gewinnen die Einsicht in die eigenen Wissensgrenzen und aktivieren ihr Vorwissen. Erst im Anschluss daran wird ihnen die Lösung präsentiert.
Wissen sichern und vertiefen
Bei der Vermittlung von Wissen kann der Einsatz von Repräsentationswerkzeugen den Schülerinnen und Schülern helfen, abstrakte Zusammenhänge leichter zu verstehen.
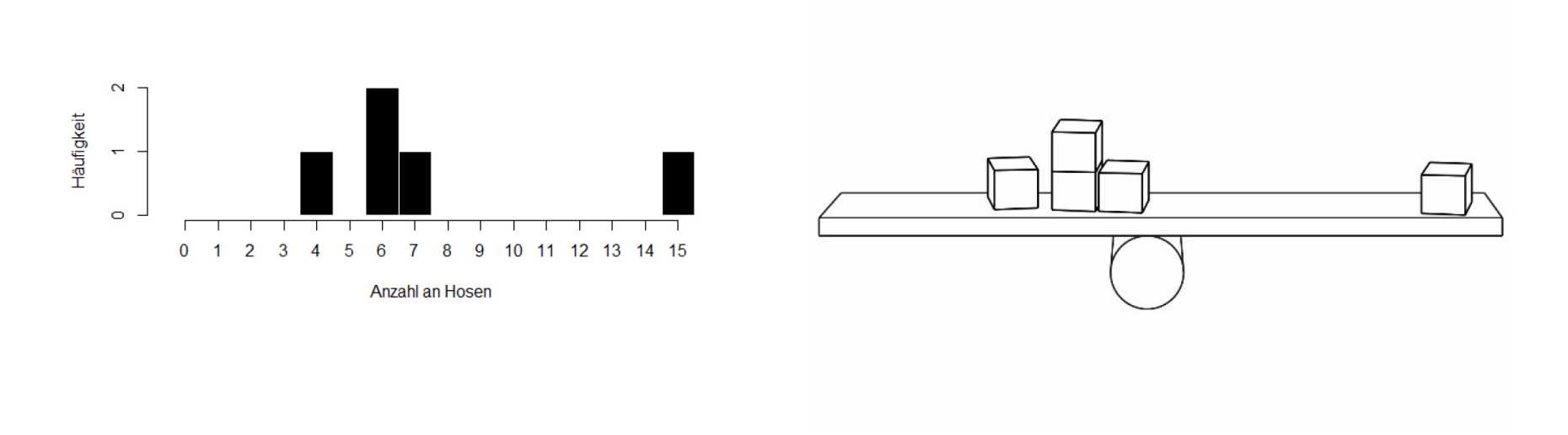
Der Schwerpunkt als Veranschaulichung des arithmetischen Mittels
Zur Veranschaulichung des arithmetischen Mittels wird häufig der Schwerpunkt verwendet:
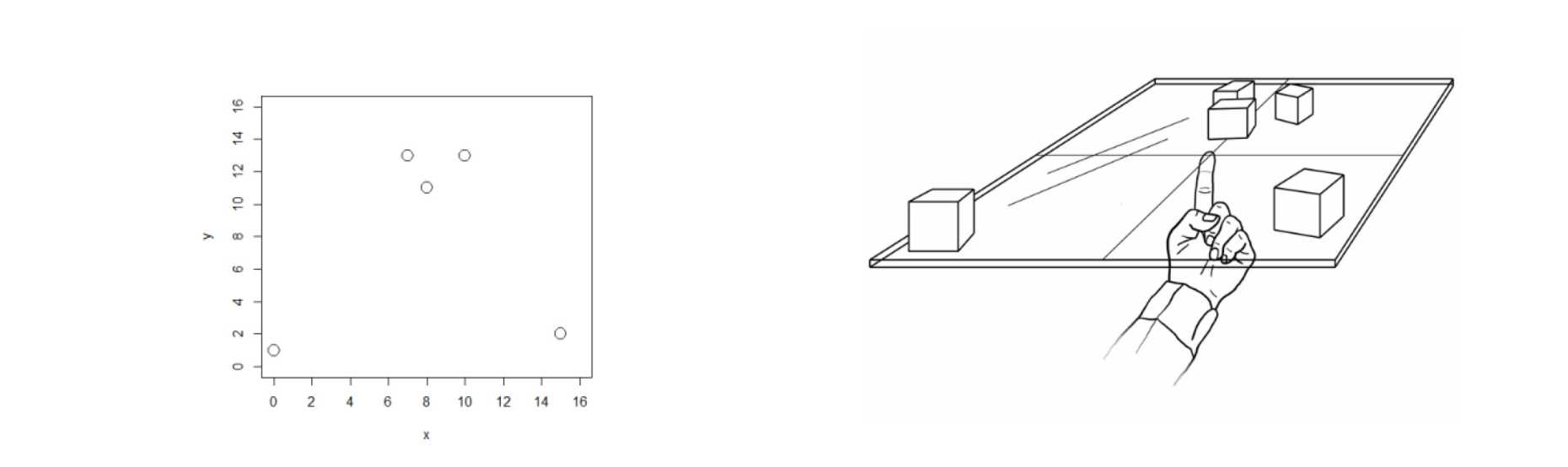
Diese Veranschaulichung wird auf Streudiagramme übertragen:
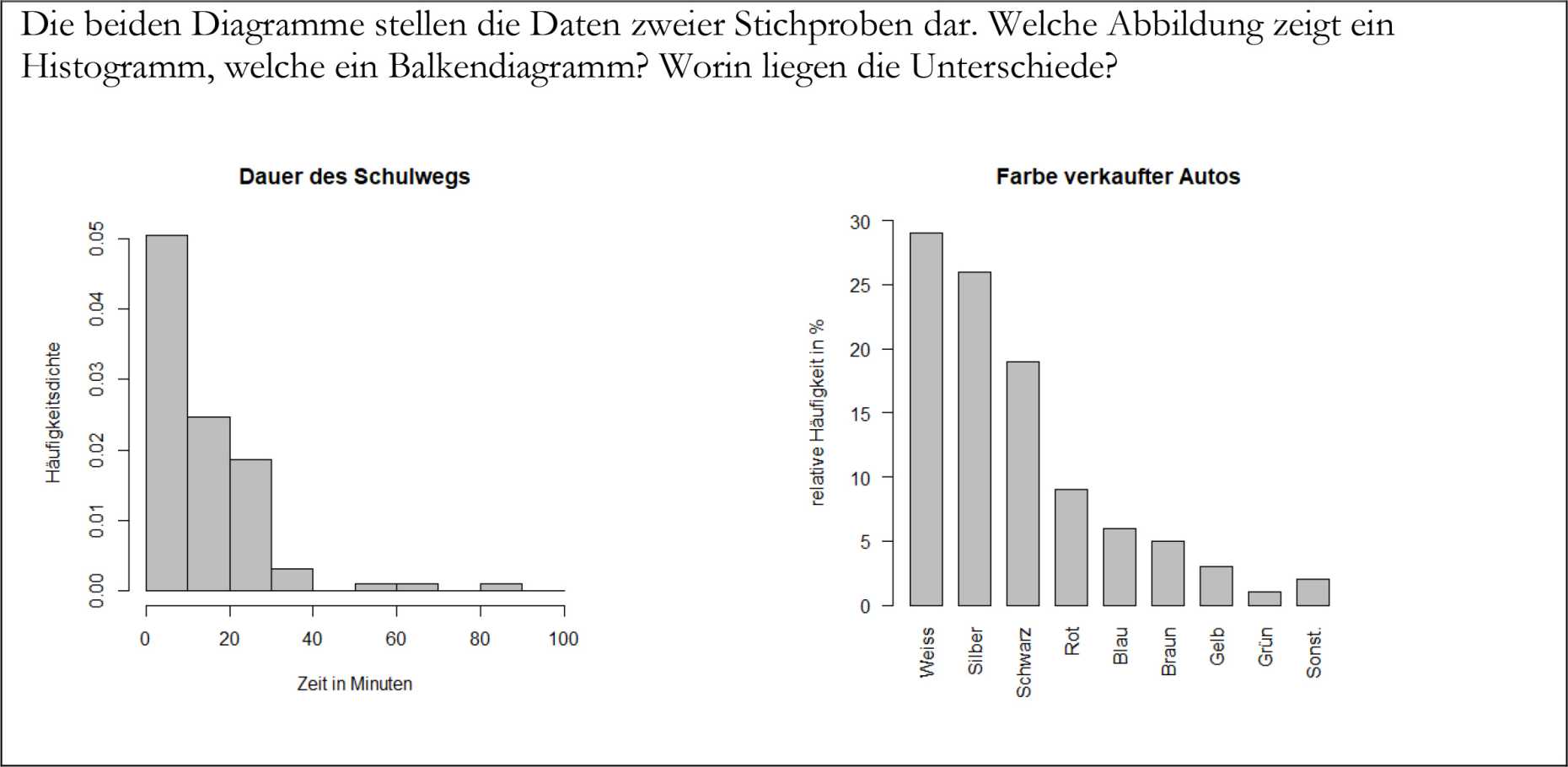
Balkendiagramm und Histogramm kontrastieren
Kontrastierungen helfen zudem, verschiedene Arten von Regeln und Darstellungsformen zu unterscheiden.
Diese Unterrichtseinheit vermittelt Schülerinnen und Schülern an Gymnasien einen nachhaltigen Einblick in die beschreibende Statistik und einen kurzen Ausblick auf die beurteilende Statistik. Dazu wurden die Unterrichtsmaterialien nach den neuesten Erkenntnissen der Lehr- und Lernforschung entwickelt. Sie enthalten neben Vorschlägen zum Aufbau der einzelnen Lektionen kognitiv aktivierende Einstiegsaufgaben und Lesetexte, welche der Lehrperson als Grundlage für den Unterricht dienen und/oder den Lernenden als Lektüre empfohlen werden können. Die Selbsterklärungs- und Anwendungsaufgaben zu jeder Sequenz sollen die Schülerinnen und Schüler dazu anregen, alle wichtigen Überlegungen selber nachzuvollziehen, um auf diese Weise das Erlernte zu festigen.
Viel Wert wurde auf den Zugang zu den gängigen Inhalten gelegt: Durch das produktive Scheitern (Productive Failure) und mit ICC (Inventing with Contrasting Cases) wird ein besseres konzeptuelles Verständnis der Schülerinnen und Schüler gefördert.
Lernziele der Unterrichtseinheit
- Die Schülerinnen und Schüler bringen oft einen sehr unterschiedlichen Katalog an statistischem Wissen in den Unterricht, aber viele sind gerne bereit, statistische Daten zu interpretieren. Daher geht es nach einem geschichtlichen Überblick darum, das Wissen zu ordnen und einige Grundbegriffe kennenzulernen. Zudem setzen sie sich mit der Datengewinnung und möglichen Fehlerquellen auseinander.
- Die Schülerinnen und Schüler können die wichtigsten Diagrammtypen interpretieren. Insbesondere wissen sie, dass neben der Strecke (z.B. Länge eines Balkens) auch die Fläche als Mass für die Häufigkeit in Diagrammen verwendet wird.
- Die Schülerinnen und Schüler können den Median, den Modus und das arithmetische Mittel als Kennzahlen für die Lage unterscheiden und bestimmen.
- Die Schülerinnen und Schüler können die Spannweite und den Quartilsabstand bestimmen. Zudem können sie die Lage und Verteilung von Daten in einem Boxplot darstellen. Sie kennen als weitere Kennzahlen der Streuung die Varianz und die Standardabweichung und können diese berechnen.
- Die Schülerinnen und Schüler lernen den Korrelationskoeffizienten als Kennzahl für den linearen Zusammenhang bei bivariaten Daten kennen und können in Anwendungen den Wert berechnen und interpretieren.
- Die Schülerinnen und Schüler lernen die Summe der quadrierten Abweichungen als Gütekriterium für Trendgeraden kennen. Sie können die Regressionsgerade als Trendgerade bei zweidimensionalen Häufigkeitsverteilungen bestimmen und anwenden.
- Die Schülerinnen und Schüler vertiefen die Unterscheidung zwischen qualitativen und quantitativen Merkmalen und erkennen, dass die Skalierung eines Merkmals wesentlich von der Erhebung der Daten abhängt.
- Die Schülerinnen und Schüler wissen, welche Datentypen bei Histogrammen und welche bei Balkendiagrammen verwendet werden können. Sie können ein Histogramm bei vorgegebener Gruppierung zeichnen und die dazu erforderlichen Häufigkeitsdichten bestimmen.