Potenzen und Wurzeln
- Nächster Termin: 19. bis 20. April 2024
- Kursleitung: Dmitrij Nikolenkov
- Autor: Armin P. Barth
- Schulstufe: 9. -10. Schuljahr, Gymnasium
- Umfang: 20- 30 Lektionen
- Kosten: 600 CHF
Anmeldung über diesen externe SeiteLINK
Die Mathematik lebt von tollen Ideen. Das zeigt sich auch am Beispiel der Potenzen mit beliebigen Exponenten deutlich. Es sind ebenso interessante wie überzeugende Ideen nötig, um das Konzept der Potenz schrittweise so zu erweitern, dass ganzzahlige, rationale oder sogar reelle Exponenten benutzt werden können. Die Unterrichtseinheit bietet den Lernenden die Gelegenheit, mit Ideen in Kontakt zu treten, die Leonhard Euler in seiner „Algebra“ (1770) in unübertrefflicher Klarheit und Prägnanz ausformuliert hat. Dank einer überaus eleganten Überlegung dieses bedeutenden Schweizer Mathematikers kann man zum Beispiel Potenzen mit negativen ganzzahligen Exponenten leicht verstehen.
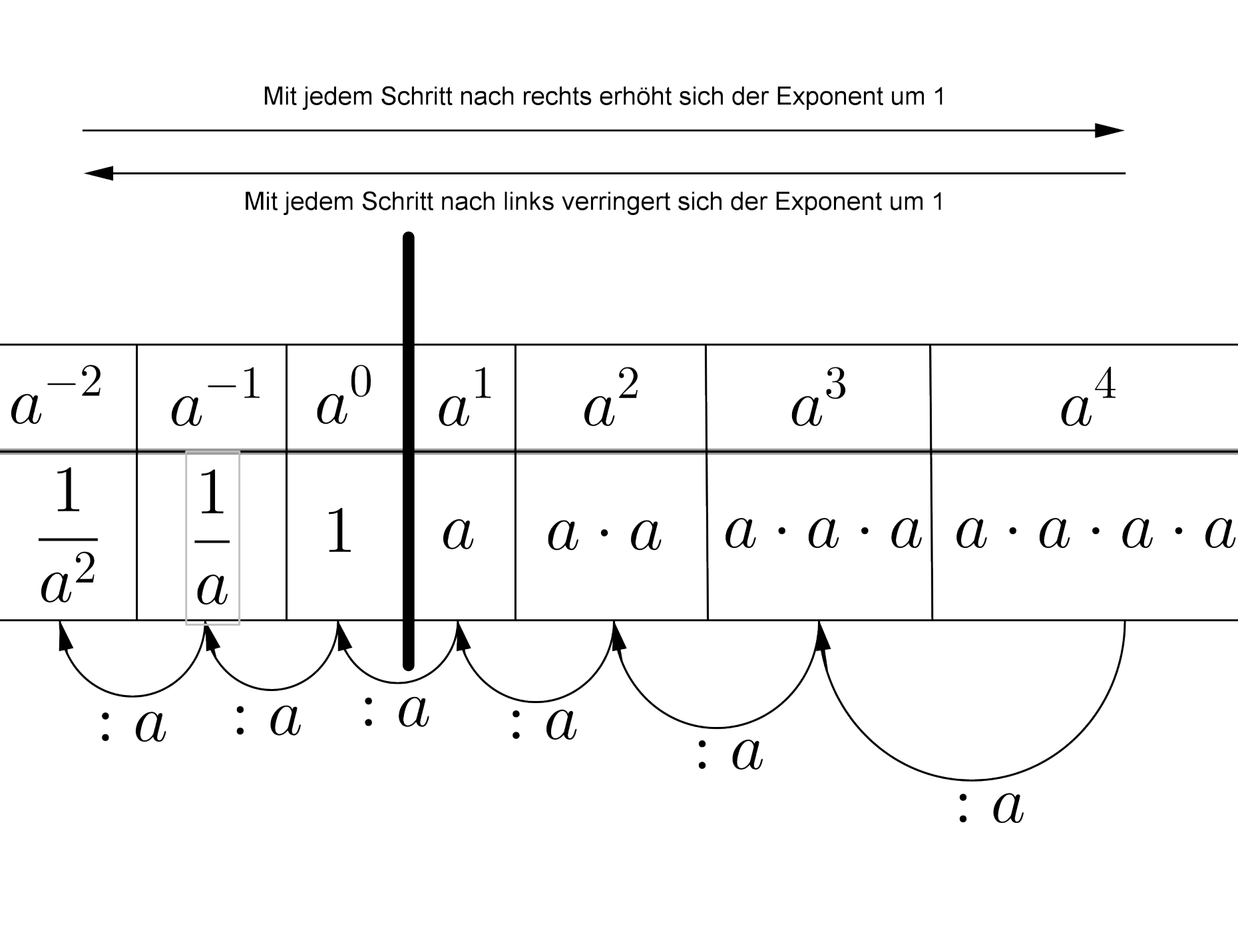
Die Abbildung macht deutlich, dass mit jedem Schritt nach rechts einerseits eine Multiplikation mit a stattfindet, andererseits aber auch der Exponent um 1 anwächst. Folglich findet mit jedem Schritt nach links eine Division durch a statt, und der Exponent verringert sich um 1. Führt man das konsequent weiter, so gelangt man unweigerlich zu Potenzen mit negativen ganzzahligen Exponenten und versteht deren Bedeutung auf Anhieb.
Wie alle Unterrichtsmaterialien des MINT-Lernzentrums zeichnet sich auch diese Einheit durch die sorgfältige Umsetzung von Lernformen aus, die sich in empirischen Vergleichsstudien als besonders lernwirksam erwiesen haben. Dazu zählen Aktivierungen des Vorwissens ebenso wie Unterrichtseinstiege, die Motivation schaffen, den Lernenden die Grenzen ihres Wissens bewusstmachen und ihnen die Möglichkeit zur eigenen Wissenskonstruktion geben. Methoden, die die Lehr- und Lernforschung als sehr erfolgreich nachgewiesen hat (wie Lernaufgaben oder problem posing) sind charakteristisch für diese Unterrichtseinheit. Die Aufträge sind so konzipiert, dass die Jugendlichen Vieles selber entdecken können. Mit Hilfe von gezielten Selbsterklärungs- und Metakognitionsaufträgen sichern die Lernenden das erarbeitete Wissen. Ein Vor- und ein Nachtest geben Auskunft darüber, was und wie viel dazu gelernt worden ist.
Diese Unterrichtseinheit eignet sich für alle Kurz- und Langzeitgymnasien und beinhaltet Material für 20- 30 Lektionen. Vorausgesetzt wird, dass die Schülerinnen und Schüler bereits eine Notation wie etwa 25 verstehen und mit dem Konzept der Quadratwurzel vertraut sind. Es wird allerdings zu Beginn eine detaillierte Wiederholung dieser Konzepte angeboten. Zudem baut die Unterrichtseinheit darauf auf, dass die Lernenden wissen, was natürliche, ganze, rationale, irrationale und reelle Zahlen sind, dass sie mit Bruchtermen umgehen können, Kenntnisse zur elementaren Algebra haben und bereits einfachen Funktionen begegnet sind.
Mit dieser Unterrichtseinheit sollen Schülerinnen und Schüler am Gymnasium nachhaltig lernen, was Potenzen mit rationalen Exponenten (darunter speziell Potenzen mit Exponent 0 und mit negativen Exponenten) sind und welchen Gesetzmäßigkeiten diese unterliegen. Sie verstehen schließlich, dass Wurzeln einfach nur spezielle Potenzen sind und können im Umgang mit ihnen die Potenzgesetze nutzbar machen. Des Weiteren erhalten sie eine fundierte Einführung in das Konzept der Potenzfunktion und loten aus, welche Eigenschaften die Graphen solcher Funktionen typischerweise haben.
Zusätzlich zu genauen Vorschlägen zum Aufbau der einzelnen Lektionen enthält die Unterrichtseinheit verschiedene kognitiv aktivierende Einstiegsaufgaben und Lesetexte, die für die Lehrperson ebenso hilfreich sind wie für die Lernenden. Viel Wert wird daraufgelegt, dass die Lernenden sich die wesentlichen Konzepte zuerst selber aneignen können und dass sie vielfältige Angebote zur Vertiefung und Wissenssicherung finden. Darum enthält die Unterrichtseinheit Selbsterklärungs- und Übungsaufgaben mit Anwendungen samt Lösungen. Aussagekräftige Tests (Vor- und Nachtest) runden das Angebot der Einheit ab.