Integralrechnung
- Nächster Termin: nach Absprache
- Kursleitung: Dmitrij Nikolenkov
- Autor: Armin Barth
- Schulstufe: 12. und 13. Schuljahr, Gymnasium
- Umfang: 30 – 40 Lektionen
- Kosten: 600 CHF
Anmeldung über diesen externe Seite LINK
Fahren Sie demnächst nach Heidelberg, um das Schloss zu besichtigen? Eine ganz besondere Attraktion im Schloss ist das Karl-Theodor-Fass, eines der grössten Weinfässer der Welt, das 1750/51 erbaut wurde und noch heute bewundert werden kann. Es ist 8 Meter lang, in der Mitte hat es einen Durchmesser von 6 Metern, und die beiden kreisförmigen Seitenflächen haben einen Durchmesser von 5 Metern. Wie seine Vorgänger hat auch dieses Fass auf seiner Oberseite einen Tanzboden.
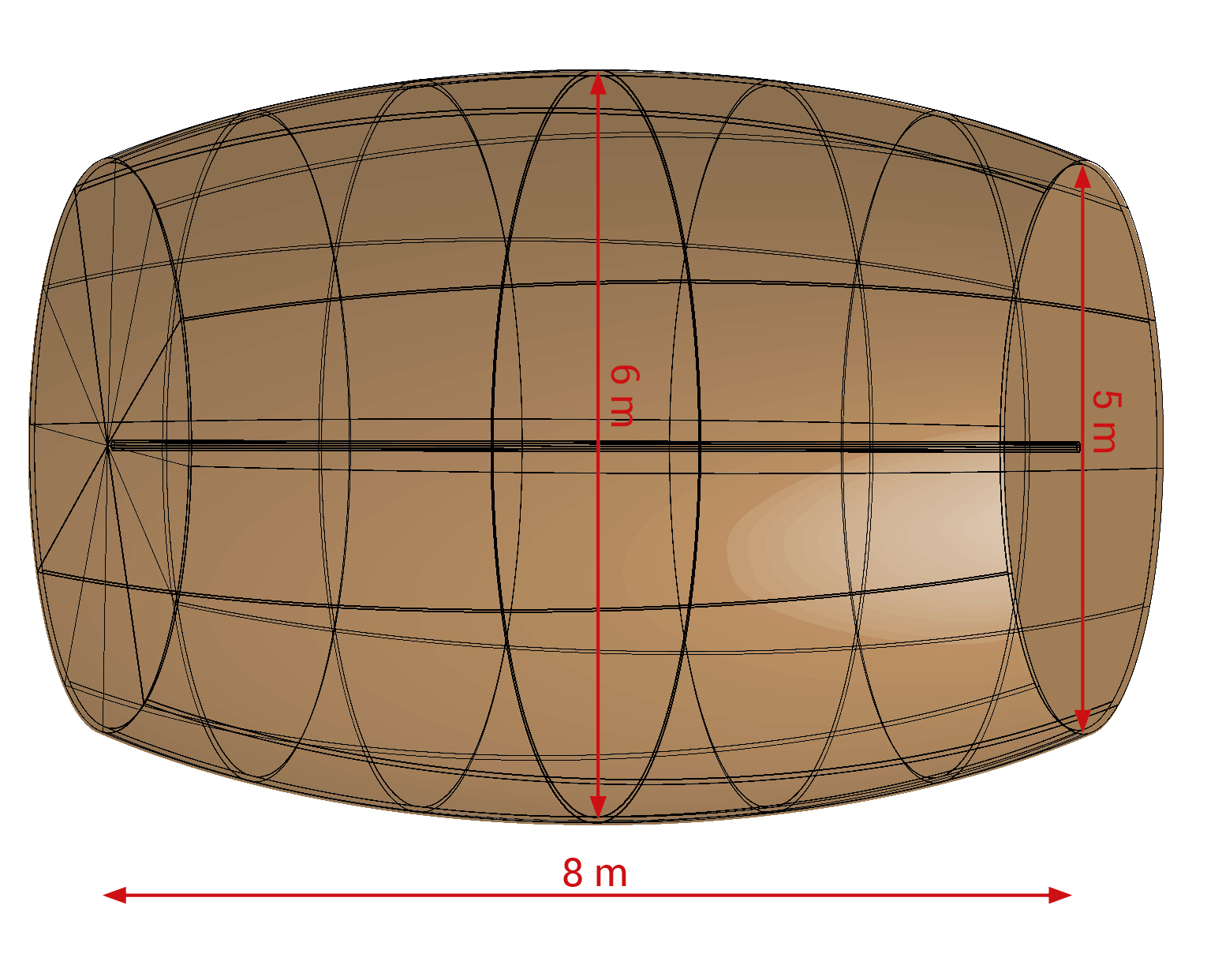
Egal, wie trinkfest Sie sein mögen, dieses Fass wird Ihren Anforderungen sicher genügen. Als es damals dazu diente, die unzähligen durstigen Kehlen am Heidelberger Hof zu befriedigen, dauerte es über 100 Tage, bis es leergetrunken war. Der Legende nach soll der Hofnarr Perkeo der Fasswächter gewesen sein. Auf die Frage, ob er das Fass allein austrinken könne, soll er auf Italienisch geantwortet haben: «Perché no?» (warum nicht?). Diese Antwort hat ihm seinen Namen eingebracht.
Wenn Sie vor dem Fass stehen, möchten Sie bestimmt wissen, wie viele Liter es fasst. Können wir das allein aus seinen Massen abschätzen?
Mit dieser Unterrichtseinheit sollen Schülerinnen und Schüler am Gymnasium die Grundlagen der Integralrechnung gut und nachhaltig lernen. Es werden Lernformen eingesetzt, die sich in empirischen Vergleichsstudien als besonders lernwirksam erwiesen haben. Die Einheit bietet kognitiv aktivierende Einstiege, Lesetexte, Aufgaben (samt Lösungen), Vertiefungsaufträge und Tests, die direkt im Unterricht eingesetzt werden können. Viel Wert wird daraufgelegt, dass die Lernenden sich die wesentlichen Konzepte zuerst selber aneignen können und dass sie vielfältige Angebote zur Vertiefung und Festigung finden. Eine grosse Anzahl von Selbsterklärungsaufgaben helfen den Lernenden, die neuen Konzepte fokussiert und in der nötigen Tiefe durchdenken zu können. Dank Metakognitionsaufträgen lernen sie, kritisch über ihren eigenen Wissensstand nachzudenken und den Lernprozess besser zu steuern. Zeitpläne helfen den Lehrpersonen, die einzelnen Lektionen gut planen zu können.
Sequenz 1: Flächeninhalte krummlinig begrenzter Gebiete
Sequenz 2: Riemannsumme und bestimmtes Integral
Sequenz 3: Berechnung eines Integrals – der steinige Weg
Sequenz 4: Eigenschaften des bestimmten Integrals
Sequenz 5: Der Hauptsatz der Differential- und Integralrechnung
Sequenz 6: Integrationsregeln
Sequenz 7: Partielle Integration und Integration durch Substitution
Sequenz 8: Flächeninhalte und Volumina von Rotationskörpern
Sequenz 9: Gemischte Anwendungen