Die Prinzipien der Thermodynamik am Beispiel der Geothermie
In dieser Unterrichtseinheit ist die Geothermie das Leitmotiv für die Behandlung der Thermodynamik. Das MINT-Lernzentrum hat gemeinsam mit dem erdwissenschaftlichen Departement der ETH Zürich eine Unterrichtseinheit entwickelt, in der die physikalischen Grundbegriffe der Thermodynamik am Beispiel von Geothermiekraftwerken eingeführt werden. Als mögliche Energiequelle der Zukunft mit technischen Herausforderungen in ihrer Umsetzung bietet die Geothermie viele Fragestellungen, die für Schülerinnen und Schüler nachvollziehbar und interessant sind. Sie stellt in der Unterrichtseinheit den sinnstiftenden Kontext dar, in den die physikalische Theorie eingebettet wird, denn die Lernenden erarbeiten sich die Prinzipien der Thermodynamik, während sie technischen Fragen nachgehen. Die Schülerinnen und Schüler sollen nach Abschluss dieser Unterrichtseinheit über ein gutes Verständnis der physikalischen Konzepte verfügen und in der Lage sein, die Leistung einer Geothermieanlage zu modellieren.
Teil 1: Geothermie als erneuerbare Energie
- Lektion 1: Stromverbrauch und Stromproduktion in der Schweiz
- Lektion 2 und 3: Wie gross ist das Energiepotential des Zürichsees?
- Lektion 4: Was ist der beste Standort für eine Geothermieanlage? Vorschau auf wichtige physikalische und geologische Grössen
Teil 2: Unser Boden als Wärmereservoir
- Lektion 5: Thermische Energiespeicher und Wärmekapazität
- Lektion 6 und 7: Die experimentelle Bestimmung der Wärmekapazität von Festkörpern
- Lektion 8 und 9: Die mikroskopische Perspektive auf Temperatur und Wärmekapazität
Teil 3: Die Energie aus dem Boden holen
- Lektion 10: Erster Hauptsatz der Thermodynamik
- Lektion 11: Wärmetransport
Teil 4: Geothermiekraftwerke: Aus Wärme elektrischen Strom produzieren
- Lektion 12 und 13: Wärmearbeitsmaschinen
- Lektion 14: Dampfmaschine und Dampfturbine
- Lektion 15: Funktionsweise einer Geothermieanlage für die Stromproduktion
- Lektion 16: Die Leistung einer Geothermieanlage modellieren
Kognitiv aktivierende Unterrichtseinstiege: Schätzfragen als Beispiel für produktives Scheitern
In dieser Unterrichtseinheit geht es darum, welches Potential geothermische Anlagen für die Stromgewinnung haben. Als Unterrichtseinstieg wird darum die Frage gestellt, wie viel Energie zum Beispiel im Zürichsee gespeichert ist. Auf diese Weise sollen die Schülerinnen und Schüler angeregt werden, eine Vorstellung für die sehr grossen Energiemengen thermischer Speicher zu entwickeln.
Zuerst tragen sie ihre Vermutungen ein und versuchen in einem zweiten Schritt, mit weiteren Abschätzungen die frei werdende Wärme zu berechnen und ihre Vermutungen zu überprüfen. Bei einer solchen Schätzaufgabe handelt es sich um eine sogenannte Fermi-Aufgabe. Diese Aufgaben sind benannt nach dem Physiker Enrico Fermi (1901-1954), der dafür bekannt war, gute Abschätzungen machen zu können, auch wenn die dazu notwendigen Informationen nicht alle vorlagen.
Bei dieser Aufgabe stehen die notwendigen Angaben zur Berechnung der frei werdenden Energie nicht zur Verfügung, weshalb die Schülerinnen und Schüler die fehlenden Grössen selbst bestimmen müssen. Dazu bestimmen sie in einem anschliessenden Experiment die Wärmekapazität von Wasser, und mit Hilfe von Landkarten berechnen sie das Volumen des Zürichsees. Unabhängig davon, ob die Lernenden die richtige Antwort finden, eignen sich solche Fermi-Aufgaben gut dafür, dass die Lernenden eine Problemstellung intensiv durchdenken, Vorwissen aktivieren und dabei ihre Wissensgrenzen bemerken.
Das Finden von geologischen und physikalischen Grössen als Beispiel für einen anregenden Unterrichtseinstieg
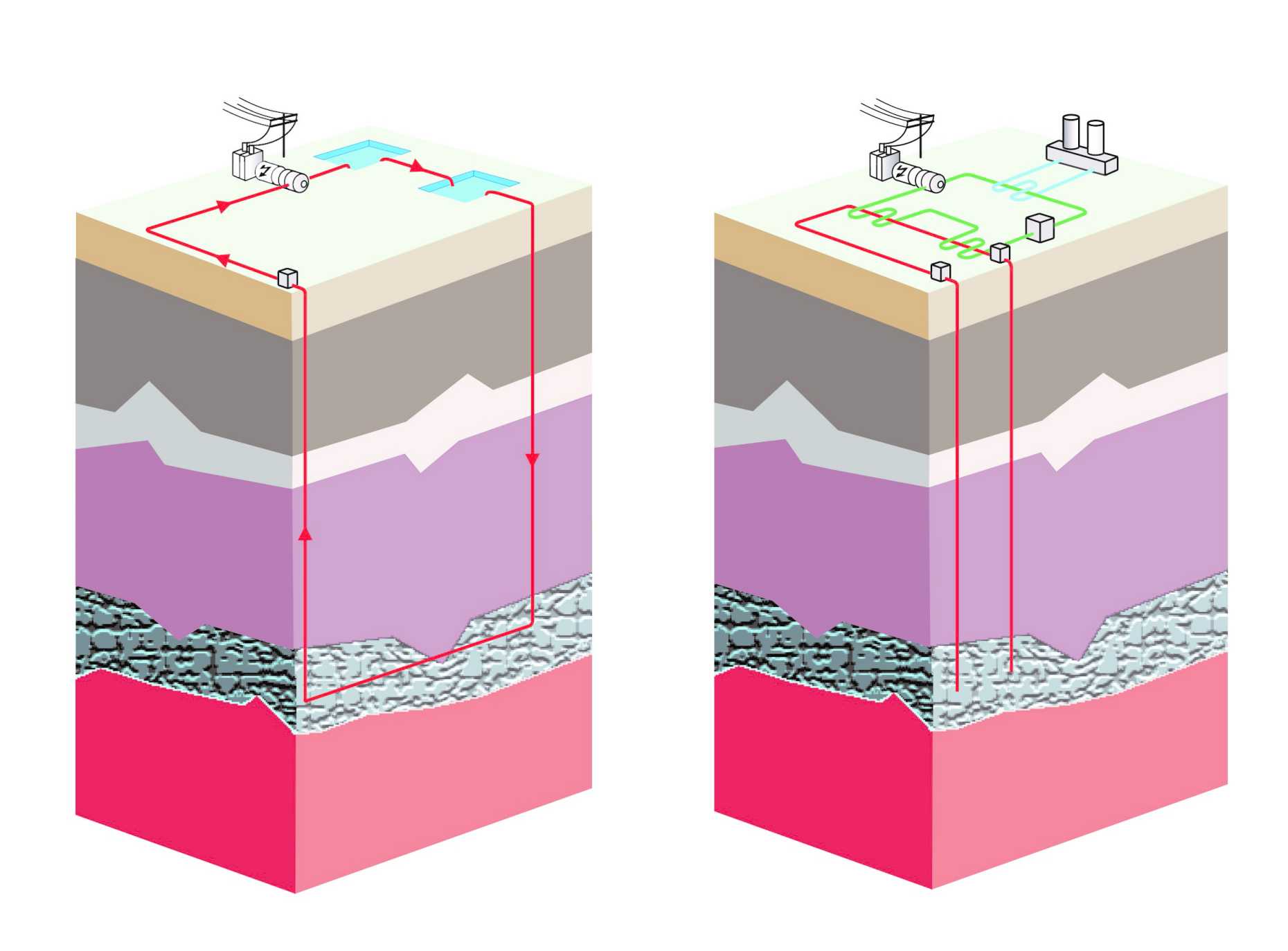
Ein anregender Unterrichtseinstieg, um die Schülerinnen und Schüler auf neue Lerninhalte vorzubereiten, ist das Finden zum Beispiel von geologischen oder physikalischen Grössen mithilfe von Kontrastierungen. Im Kasten unten ist eine solche Aufgabe dargestellt. Die Lernenden werden dazu aufgefordert, durch Kontrastierungen mehrere Gütekriterien für einen Geothermiestandort zu finden und die geologischen und physikalischen Grössen in Worten und Zeichnungen zu charakterisieren.
Sie werden beauftragt, in der Schweiz einen geeigneten Ort für eine Geothermieanlage für die Stromerzeugung zu finden. Überlegen Sie sich drei Eigenschaften, die der Boden haben sollte, damit die Geothermieanlage eine möglichst grosse Leistung über einen langen Zeitraum erbringen kann. Beschreiben Sie diese drei Eigenschaften und stellen Sie sie grafisch dar, indem Sie jeweils im linken Kasten die Eigenschaft in einer hohen (H) Ausprägung und im rechten Kasten in einer niedrigen (N) Ausprägung zeichnen.

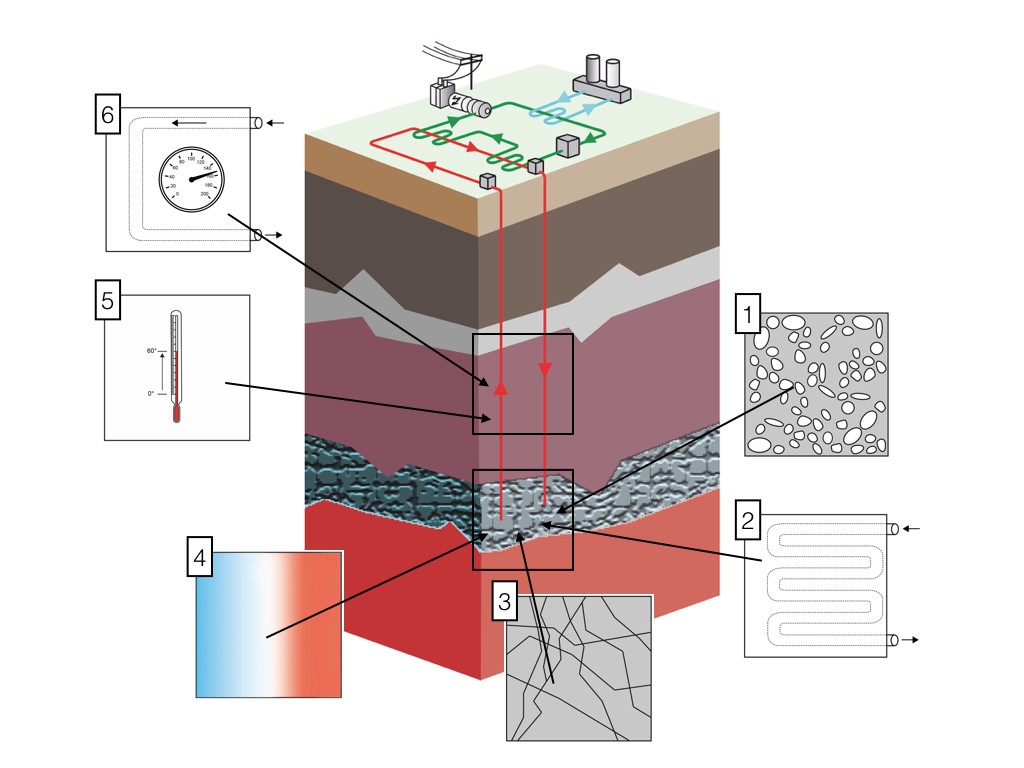
Nachdem sie sich selber drei geologische oder physikalische Grössen überlegt haben, werden den Lernenden mehrere Grössen präsentiert, die tatsächlich als Gütekriterien für Geothermiestandorte herangezogen werden. Als Beispiele dienen hier die Porosität, die Wärmeleitfähigkeit und die Wärmekapazität. Einige Grössen werden die Lernenden bereits selbst entwickelt und beschrieben haben. An andere Grössen wiederum werden sie nicht gedacht haben. Dennoch lässt sich auch an die neuen Begriffe leichter anknüpfen, weil die Lernenden über das Grundproblem einer effizient funktionierenden Geothermieanlage bereits gründlich nachgedacht haben.
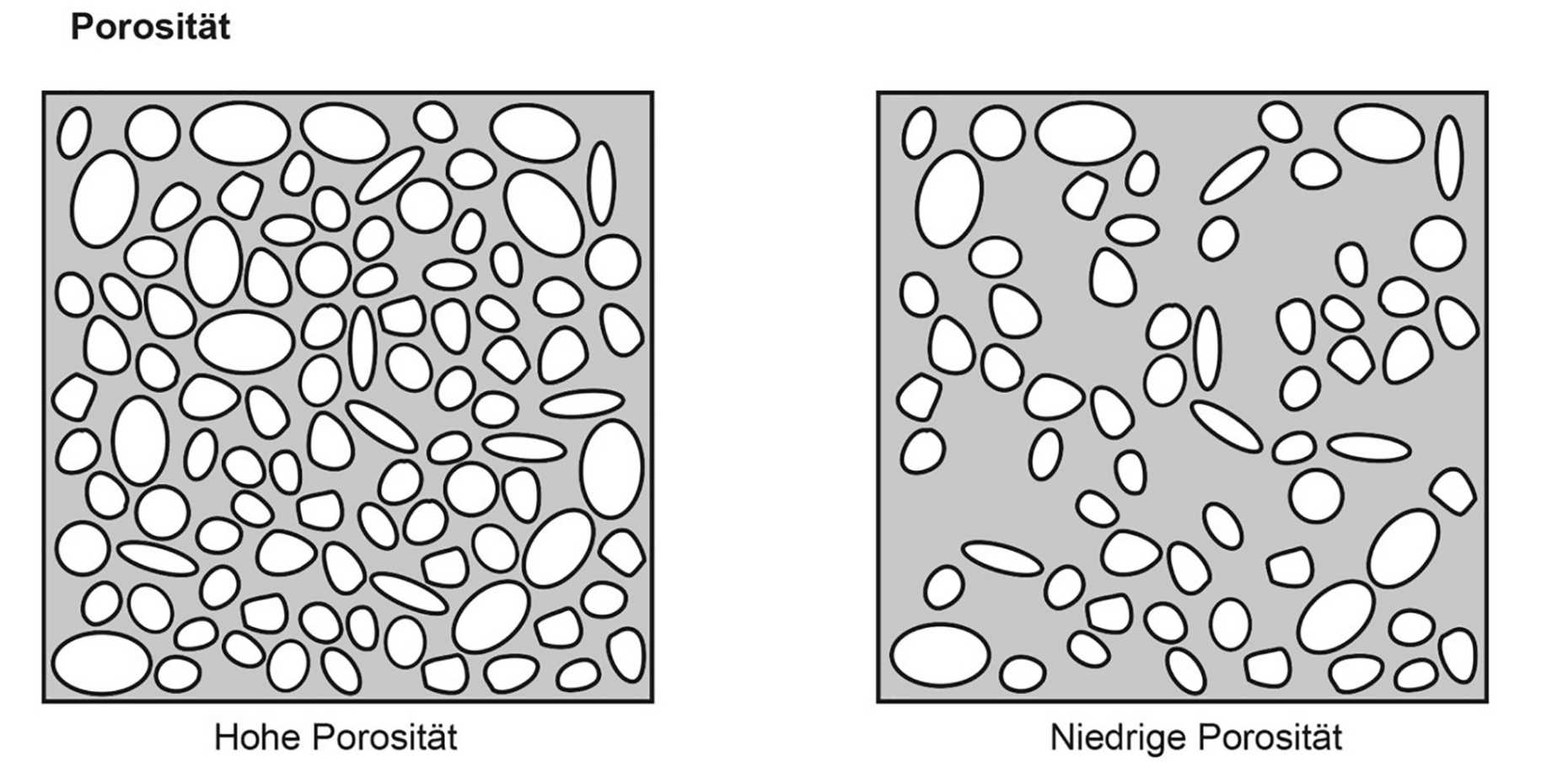
Porosität
Gesteine weisen Hohlräume in Form von Rissen, Klüften oder Poren auf. Wie gross der Anteil solcher Hohlräume in Bezug auf das Gesamtvolumen ist, wird durch die Porosität beschrieben. Sedimente wie zum Beispiel Sandstein oder Kalkstein sind um das Zehnfache poröser als magmatische Tiefengesteine, wie zum Beispiel Granit. Je poröser das Gestein ist und je grösser der Anteil der Hohlräume ist, die miteinander verbunden sind, desto eher hat das Gestein die Eigenschaften eines Schwammes und kann Flüssigkeiten oder Gase gut speichern. Im Falle der Geothermie ist es das Wasser, das in den Hohlräumen des heissen Gesteins erhitzt werden soll. Je poröser das Gestein ist, desto mehr Wasser kann erhitzt werden.
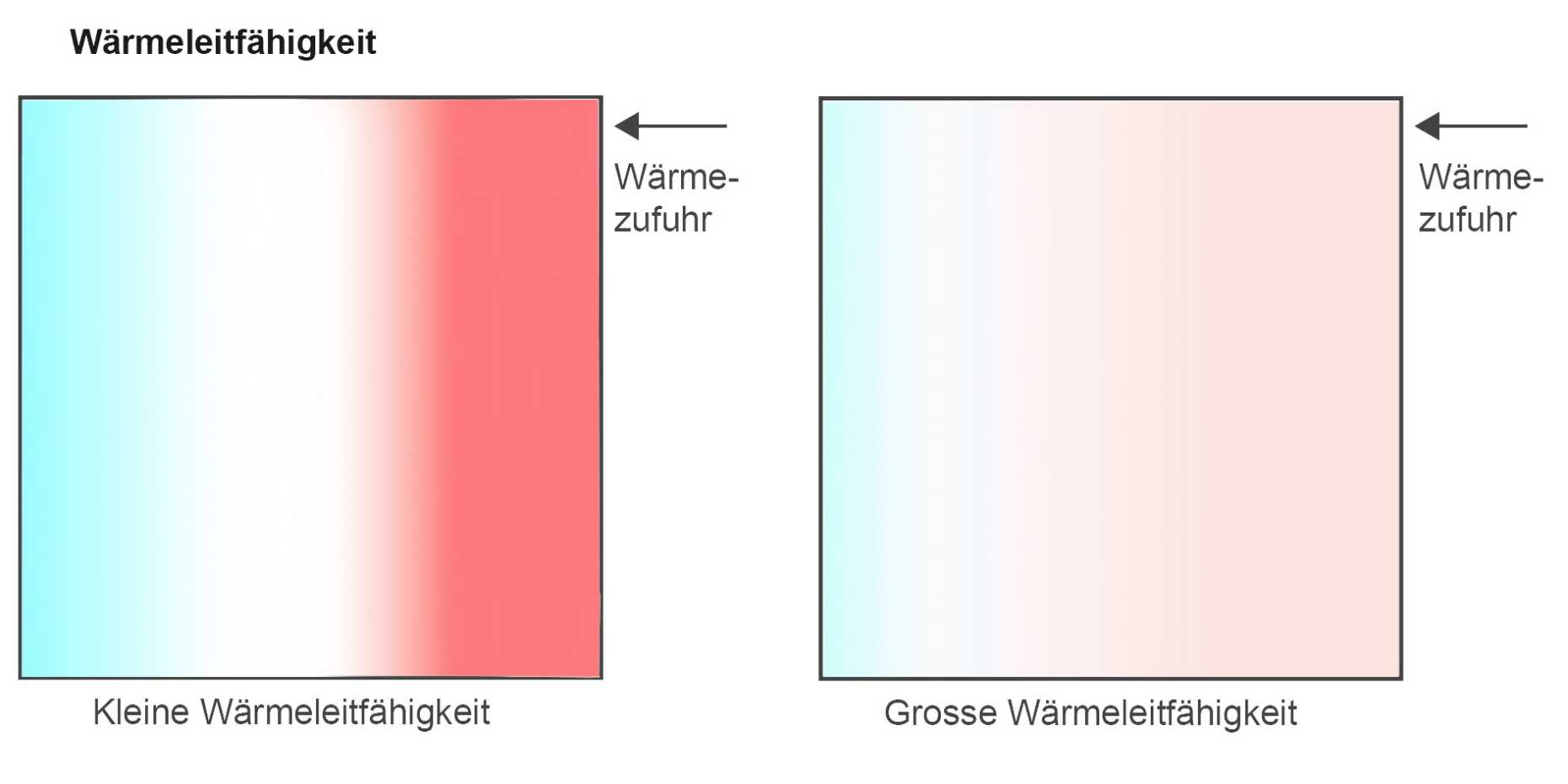
Wärmeleitfähigkeit
Die Wärmeleitfähigkeit beschreibt, wie gut ein Körper Wärme leiten kann. Der materialabhängige Wert gibt an, wie viel Wärme pro Quadratmeter und pro Sekunde durch einen 1 m breiten Körper fliesst, wenn der Temperaturunterschied zwischen den Enden 1 K beträgt. Führen wir zwei Körpern mit unterschiedlichen Wärmeleitfähigkeiten jeweils die gleiche Wärmemenge zu, so wird im Körper mit der grösseren Wärmeleitfähigkeit die Wärme schneller zum kalten Ende fliessen, weil der Wärmestrom bei höherer Wärmeleitfähigkeit grösser ist. Statt einen kalten Körper zu betrachten, den wir erhitzen, können wir uns auch umgekehrt vorstellen, dass wir einen heissen Körper auf einer Seite kühlen, indem wir ihn zum Beispiel mit kaltem Wasser in Kontakt bringen. Je geringer die Wärmeleitfähigkeit ist, desto schlechter fliesst die Wärme von der heissen Seite zur kühlen Seite nach.
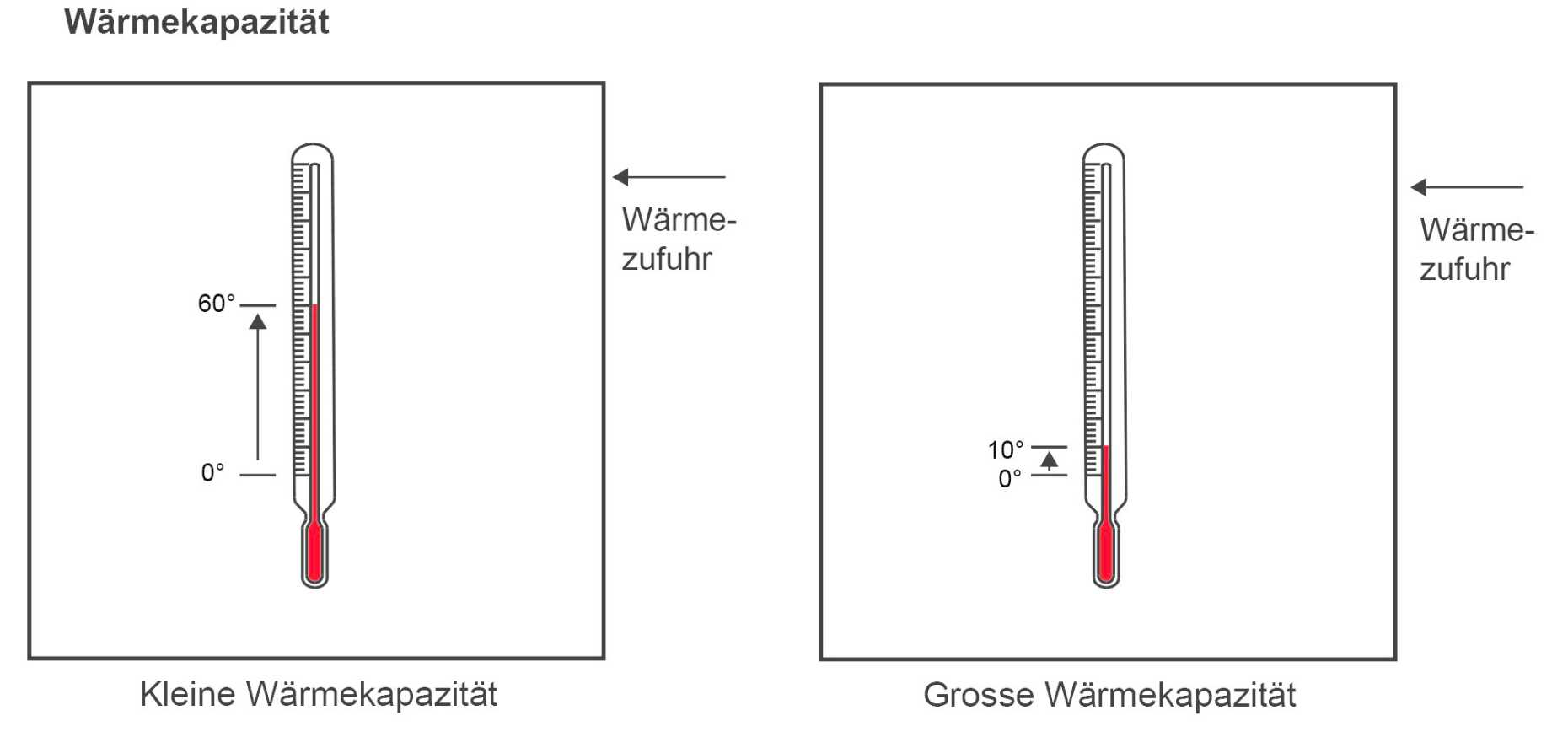
Wärmekapazität
Wird einem Körper Wärme zugeführt, so wird dadurch entweder seine Temperatur erhöht, oder die zugeführte Wärme führt zu einer Änderung des Aggregatzustandes, wie zum Beispiel beim Übergang vom flüssigen in den gasförmigen Zustand.
Die Wärmekapazität eines Körpers beschreibt, wie gut ein Körper Wärme speichern kann. Bei einem Körper mit hoher Wärmekapazität muss viel Wärme zugeführt werden, damit seine Temperatur steigt. Ein Körper mit einer hohen Wärmekapazität kann folglich bereits mit einem kleinen Temperaturanstieg viel Energie aufnehmen. Wenn also zwei Körpern mit unterschiedlicher Wärmekapazität die gleiche Wärmemenge zugeführt wird, dann kommt es beim Körper mit der höheren Wärmekapazität zu einem geringeren Temperaturanstieg als beim Körper mit der geringeren Wärmekapazität.
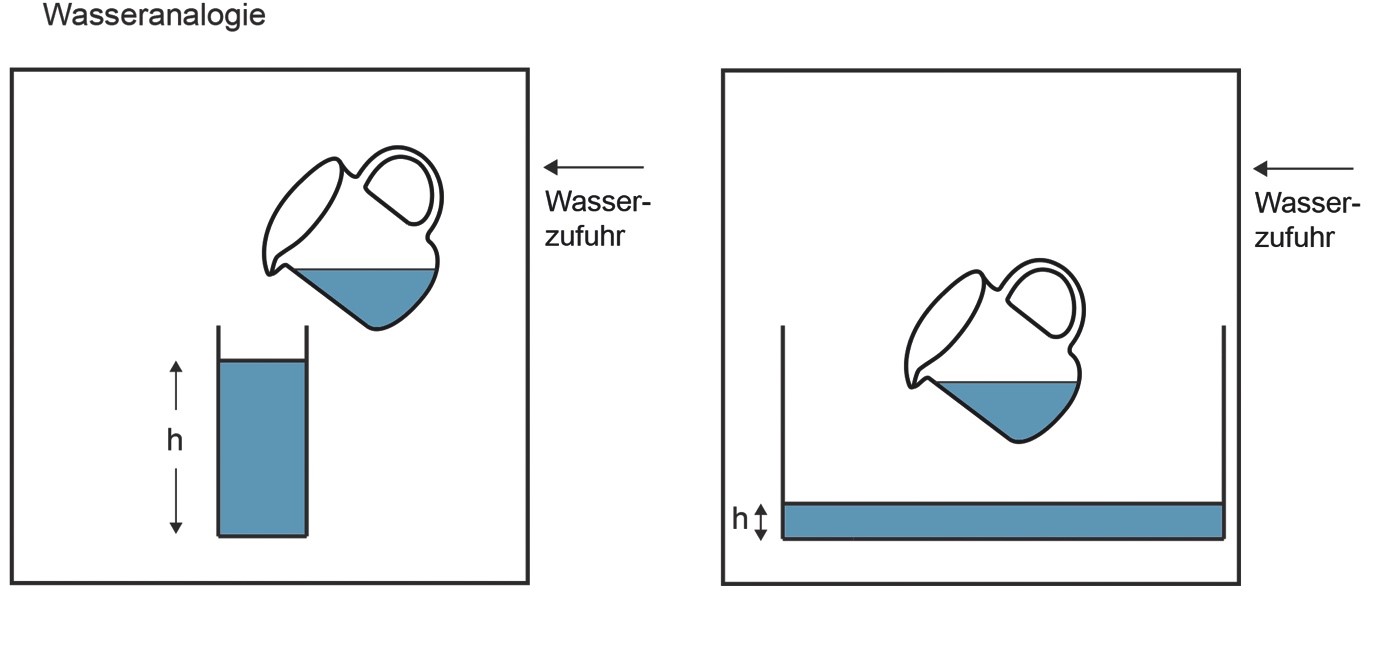
Zur Veranschaulichung kann man sich als Analogie zwei zylindrische Gefässe mit verschieden grosser Querschnittsfläche vorstellen.
Giesst man in diese Gefässe jeweils die gleiche Wassermenge, so steht das Wasser beim Gefäss mit der grossen Querschnittsfläche weniger hoch als beim Gefäss mit der kleinen Querschnittsfläche. Mit einer grösseren Querschnittsfläche kann also mehr Wasser pro Höhenunterschied gespeichert werden. Entsprechend kann mit einer grösseren Wärmekapazität mehr Wärme pro Temperaturunterschied gespeichert werden.
Nutzung von Kontrastierungen zur Abgrenzung neu gelernter Begriffe
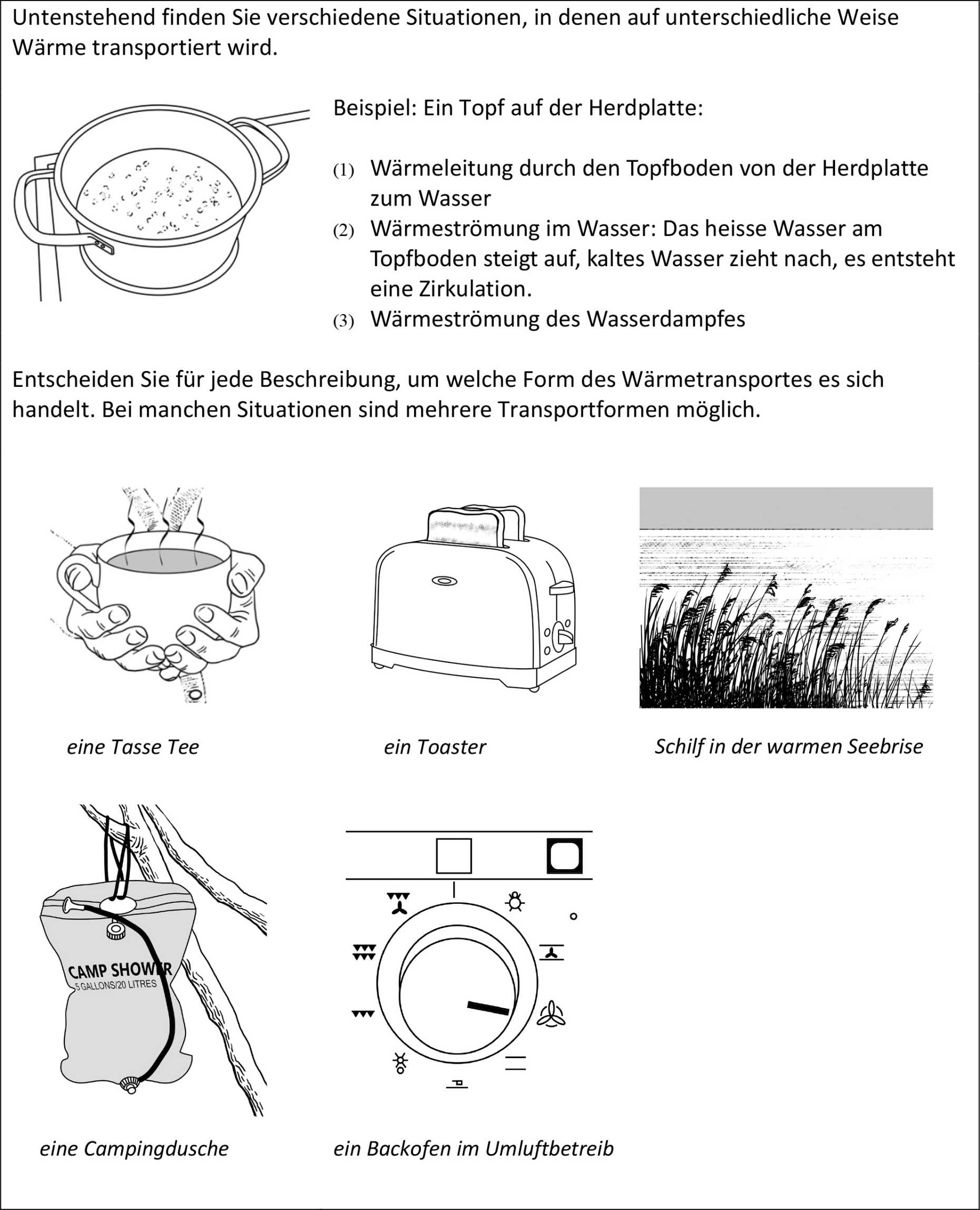
Kontrastierungen eignen sich auch dazu, neu gelernte Begriffe besser voneinander abzugrenzen. Beim untenstehenden Aufgabenblatt werden den Schülerinnen und Schülern verschiedene Fälle präsentiert, bei denen es um unterschiedliche Formen des Wärmetransports geht. Anhand dieser Beispiele sollen sie darin Sicherheit gewinnen, die drei verschiedenen Mechanismen des Wärmetransports: Wärmeleitung, Wärmeströmung, Wärmestrahlung, voneinander abzugrenzen.
Nutzung von geistigen Repräsentationswerkzeugen wie Diagrammen
In der Geothermie-Unterrichtseinheit wird mit den Schülerinnen und Schülern erarbeitet, wie sich die Wärmekapazität für Festkörper bestimmen lässt. Sie bemerken zunächst, dass sich bei Festkörpern im Unterschied zu Flüssigkeiten die Wärmezufuhr und der Temperaturanstieg nicht direkt messen lassen und dass sich deshalb die Wärmekapazität nicht so einfach ermitteln lässt. Damit sich die Schülerinnen und Schüler das alternative Vorgehen plausibel machen können, werden im Arbeitsblatt Diagramme als geistige Repräsentationswerkzeuge eingesetzt. Wie unten in Kasten präsentiert, überlegen sich die Lernenden dazu, was passiert, wenn ein heisser Stein in kaltes Wasser gelegt wird, und skizzieren den Temperaturverlauf des heissen Steins und des kalten Wassers.
Mit Hilfe des Diagramms können die Lernenden einsehen, dass sie die Endtemperatur des Steins über die Endtemperatur des Wassers indirekt bestimmen können. Genauso verfährt man mit der Bestimmung der Anfangstemperatur, wenn man den Stein zuerst in einem heissen Wasserbad erhitzt. Beim Abkühlen wird Wärme vom Stein an das Wasser abgegeben - und zwar solange, bis sich das thermische Gleichgewicht eingestellt hat. Mit diesen Vorüberlegungen können die Schülerinnen und Schüler aus der bereits bekannten Wärmekapazität des Wassers und dessen Temperaturanstieg berechnen, wie viel Wärme das Wasser vom Stein aufgenommen hat. Auf diese Weise ist es möglich, den Temperaturabfall des Steins und die abgegebene Wärme des Steins indirekt zu ermitteln und daraus die Wärmekapazität des Steins zu berechnen.
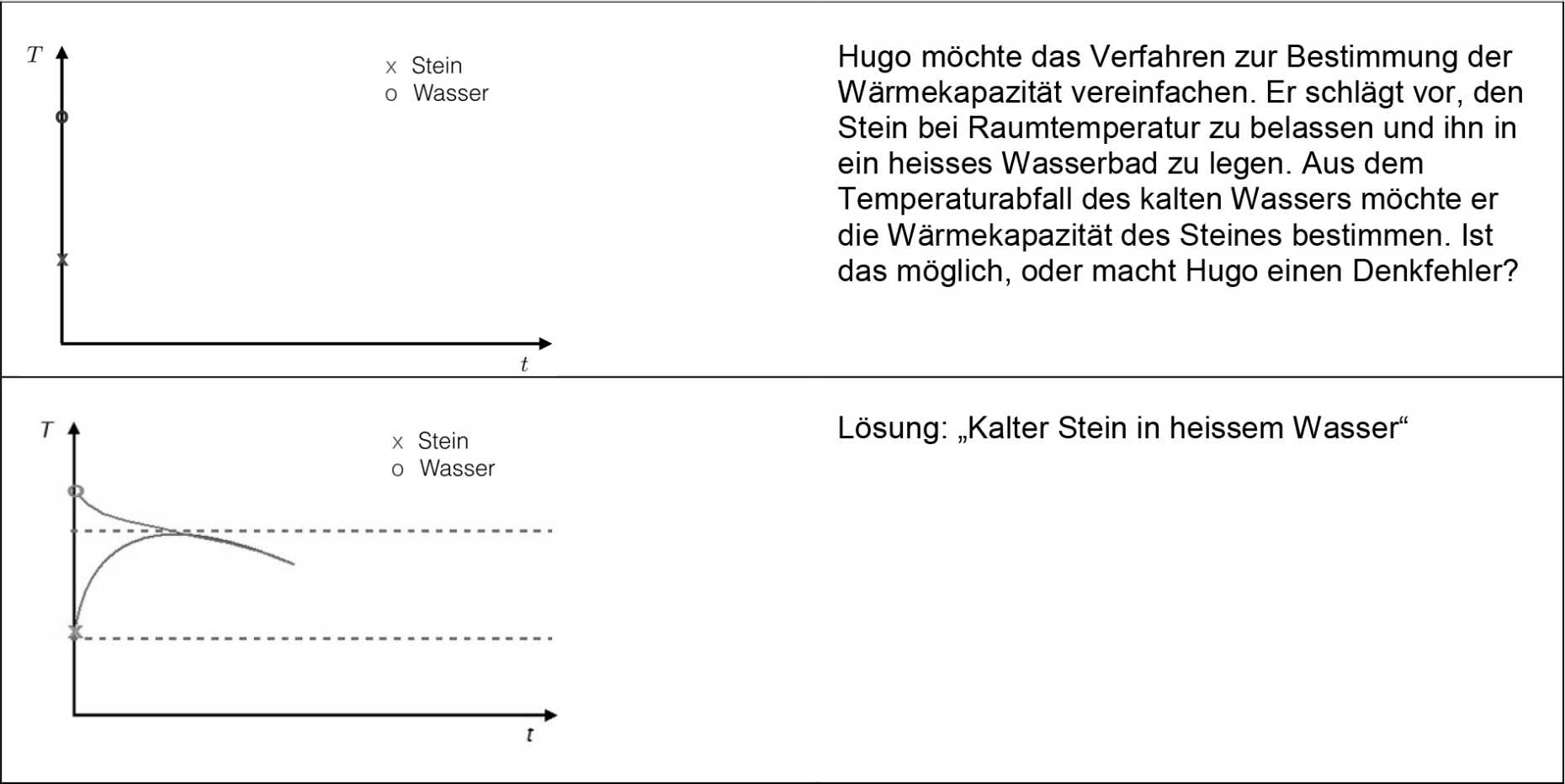
Manche Schülerinnen und Schüler glauben, es sei unnötig, den Stein zuerst in einem Wasserbad zu erhitzen. Um diese Fehlvorstellung aufzugreifen und zu beseitigen, wurde die folgende Aufgabe im nächsten Kasten gestaltet. Hier tritt der fiktive Laie Hugo auf, der in den MINT-Unterrichtseinheiten jeweils falsche Ansichten auf überzeugende Weise vertritt. Das geistige Werkzeug der Temperaturdiagramme hilft hier den Lernenden, Hugo zu erklären, weshalb sein Vorschlag nicht funktioniert.
Da für das Experiment keine perfekte Wärmedämmung realisiert werden kann, nimmt die Wassertemperatur weiter ab, auch wenn sich der Stein und das Wasser im thermischen Gleichgewicht befinden. Es bleibt deshalb unklar, welche Temperatur für die Endtemperatur des Wassers und des Steins genommen werden soll. Ist hingegen der Stein heiss und das Wasser kalt, so befinden sich Stein und Wasser dann im thermischen Gleichgewicht, wenn das Wasser das Temperaturmaximum erreicht hat. Ausserdem werden die Wärmeverluste umso grösser, je grösser die Temperaturdifferenz zwischen dem System „Wasser und Stein“ und der Raumtemperatur ausserhalb des Isoliergefässes ist. Deshalb sind die Wärmeverluste kleiner, wenn das Wasser im Isoliergefäss zu Beginn Raumtemperatur hat (siehe die letzte Abbildung).
Holistischer Vergleich zweier Modelle
Zum Abschluss der Geothermie-Unterrichtseinheit lernen die Schülerinnen und Schüler, wie eine Geothermieanlage für die Stromproduktion aufgebaut ist und wie sie funktioniert. Zur Vertiefung erhalten sie den Auftrag, das korrekte Modell, das sie im Unterricht bereits kennengelernt haben, mit einem Laienmodell zu kontrastieren und sich zu überlegen, in welchen Punkten sich die beiden Modelle unterscheiden.