Mathematik
Weitere Kursangebote zu mathematischen Themen finden Sie auf den Webseiten der ETH Math Youth Academy: ETH Math Youth Academy
Nächster Termin: Samstag, 01. Juni 2024, 09 – 16 Uhr
Umfang: 7 Lektionen
Schulstufe: ab dem 10. Schuljahr
Kursleitung: Mojgan Hosseinzadeh
Veranstaltungsort: ETH Zürich, 8092 Zürich. Der genaue Veranstaltungsort wird kurz vor Kursbeginn bekanntgegeben, damit wir die Raumgrösse flexibel planen können.
Anmeldung: externe Seitezum Anmeldeformular
Sie können sich bis zu zwei Tage vor Kursbeginn anmelden. Melden Sie sich bei Schwierigkeiten unter bei uns.
Dieser Kurs befasst sich mit den Basiselementen der beschreibenden Statistik.
Jeder weiss, wie man den Durchschnitt, auch arithmetisches Mittel genannt, berechnen kann. Allerdings sagt einem das arithmetische Mittel nichts darüber, wie die Werte um den Mittelwert verteilt sind. Dazu braucht man das mathematische Konzept der Standardabweichung.
Die Standardabweichung: Wie kann ich zum Beispiel ein gutes Bild von der Notenverteilung einer Klasse erhalten?
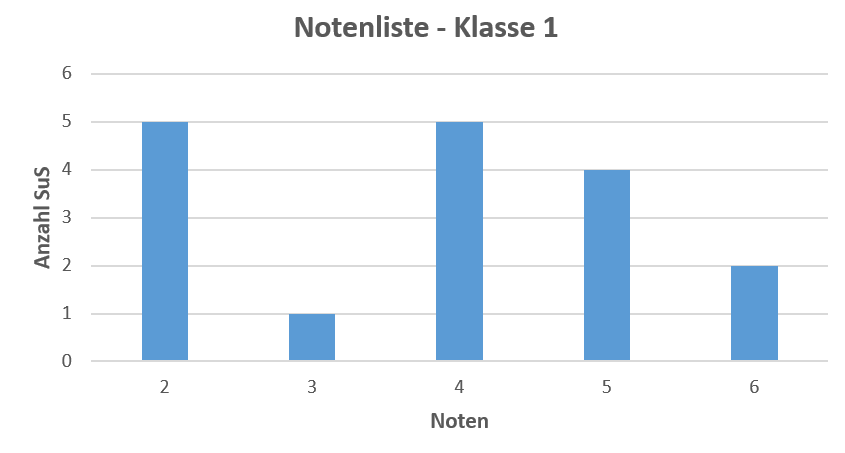
Das Diagramm zeigt die Noten von 13 Schüler*innen einer Klasse. Die Zahlen 2 bis 6 auf der horizontalen Achse entsprechen den verteilten Noten, die Zahlen 0 bis 6 auf der vertikalen Achse entsprechen der Anzahl der Schüler*innen, welche die jeweilige Note erhalten haben.
Indem wir die Standardabweichung berechnen, können wir herausfinden, ob sich die Noten gleichmässig um den Notendurchschnitt verteilen.
Das Standardisieren: Wie kann ich die Ergebnisse verschiedener Tests miteinander vergleichen?
Cécile ist eine ambitionierte Leichtathletin und steht vor der Entscheidung, ob sie sich auf einzelne Disziplinen spezialisieren möchte. Sie hat sich dazu schon einige Gedanken gemacht und möchte ihre Resultate beim letzten Wettkampf berücksichtigen. Cécile lag beim 5-Kampf, insbesondere beim Kugelstossen mit einer Weite von 13.55 m und beim Hochsprung mit einer Höhe von 1.85 m vorne mit dabei.
In den beiden Tabellen sind die Ergebnisse aller Sportlerinnen beim 5-Kampf-Wettkampf aufgeführt:
In welcher Disziplin war Cécile im Vergleich zu ihrer Konkurrenz besser? Wie kann man die Leistungen beim Hochsprung mit den Leistungen beim Kugelstossen vergleichen? Um einen solchen Vergleich durchführen zu können, müssen wir die Daten zuerst standardisieren. Wie man das macht, werden wir im Kurs besprechen.
Korrelation: Welche Zusammenhänge gibt es zwischen den verschiedenen Disziplinen?
Hier haben wir die Leistungen von fünf Leichtathletinnen in allen Disziplinen des 5-Kampfes. Gibt es Disziplinen, die miteinander zusammenhängen? Man könnte zum Beispiel vermuten, dass jemand, der gut im 60-Meter-Hürdenlauf ist, auch im 800-Meter-Lauf gute Leistungen zeigt. Oder gibt es einen Zusammenhang zwischen Hoch- und Weitsprung?
Um solche Zusammenhänge herauszufinden, brauchen wir das mathematische Konzept der Korrelation, auf das in diesem Kurs ebenfalls ausführlich eingegangen wird.
Nächster Termin: Donnerstags, 27. Juni – 11. Juli 2024, 16 – 18 Uhr
Umfang: drei Treffen mit jeweils einer Doppellektionen (6 Lektionen)
Schulstufe: ab dem 8. Schuljahr
Kursleitung: Lorenz Stäheli
Veranstaltungsort: ETH Zürich, 8092 Zürich. Der genaue Veranstaltungsort wird mit der Anmeldung bekanntgegeben, damit wir die Raumgrösse flexibel planen können.
Anmeldung: externe Seitezum Anmeldeformular
Sie können sich bis zu zwei Tage vor Kursbeginn anmelden. Melden Sie sich bei Schwierigkeiten unter bei uns.
Dieser Kurs bietet eine spielerische Einführung in die Wahrscheinlichkeitsrechnung für Schülerinnen und Schüler ab dem 8. Schuljahr. Wir werden mit vielen Beispielen wie den folgenden erkunden, mit welchen Mitteln man die Wahrscheinlichkeit von Ereignissen berechnen kann. Schaut Euch mal die folgenden drei Beispiele an und überlegt Euch, wie Ihr die Wahrscheinlichkeiten einschätzt. Die Lösungen findet Ihr ganz unten auf der Webseite.
Beispiel 1: Roulette
Beim Roulette gibt es 37 Zahlen von 0 bis 36. Wie gross ist die Wahrscheinlichkeit, dass die Kugel nicht auf die Null fällt?
Die Wahrscheinlichkeit beträgt:
a) 1/37
b) 36/37
c) 1/2
Beispiel 2: Würfel
Die Wahrscheinlichkeit, mit einem Würfel eine bestimmte Augenzahl zu werfen, beträgt 1/6. Wirft man zwei Würfel, so kann man aus den beiden Augenzahlen die Augensumme bilden. Die Abbildung zeigt die Augensumme 3.
Wie gross ist die Wahrscheinlichkeit, mit zwei Würfeln die Augensumme 3 zu werfen?
Die Wahrscheinlichkeit beträgt:
a) 3/12
b) 1/3
c) 1/18
d) 2/6
Beispiel 3: Tochter oder Sohn?
Wenn ich Euch verrate, dass ich zwei Kinder habe und dass eines davon ein Mädchen ist, wie gross schätzt Ihr dann die Wahrscheinlichkeit, dass mein zweites Kind ein Junge ist?
Die Wahrscheinlichkeit beträgt:
a) 2/3
b) 1/2
c) 1/4
Wenn Euch diese Fragen interessieren, dann kommt zu unserem Kurs. Wir werden Euch erklären, wie man zum Beispiel mithilfe von Baumdiagrammen diese Fragen beantworten kann. Natürlich wird dabei auch gespielt!
Dies sind die richtigen Lösungen: Beispiel 1: b, Beispiel 2: c, Beispiel 3: a. Habt Ihr das auch so eingeschätzt?
Inhaltsübersicht
- Zufall und Wahrscheinlichkeit:
Zuerst wird die Frage beantwortet, wie man bei einfachen Spielen die Wahrscheinlichkeit bestimmen kann. Einfache Spiele meint hier, dass alle Ergebnisse gleich wahrscheinlich eintreten, wie zum Beispiel beim Würfel die sechs verschiedenen Augenzahlen. Die Wahrscheinlichkeit lässt sich dann als Verhältnis aus den günstigen zu den möglichen Fällen bestimmen. Zur Veranschaulichung werden wir auch das sogenannte Urnenmodell kennenlernen: Das ist ein Gefäss mit mehreren Kugeln, aus dem eine Kugel zufällig gezogen wird.
- Kombinatorik:
Soll ein Passwort aus sechs Buchstaben bestehen, so gibt es über 300 Millionen Möglichkeiten. All die Wörter aufzuschreiben und sie dann zu zählen, will niemand. Vielmehr beginnt man gleich durch kombinatorische Überlegungen, die Anzahl zu berechnen. Bei der Kombinatorik versuchen wir also, die Anzahl der Möglichkeiten zu bestimmen, ohne zu zählen. Dabei hilft uns das Urnenmodell, verschiedene Situationen zu unterscheiden.
- Mehrstufige Zufallsexperimente:
Zum Schluss betrachten wir Spiele, die aus mehreren Spielen oder aus der Wiederholung des gleichen Spiels bestehen. Beispiele dafür sind das viermalige Werfen einer Münze oder das zufällige Öffnen einer von drei Schubladen und das Ziehen eines Sockens in einem dunklen Zimmer. Die Wahrscheinlichkeiten bei jedem einzelnen Schritt können wir bereits angeben und die verschiedenen Möglichkeiten können wir mit Hilfe der Kombinatorik überlegen. Mit Hilfe des Baumdiagramms werden wir lernen, die Wahrscheinlichkeiten für ein Ereignis zu berechnen.
Nächster Termin: Wir werden in Kürze einen Termin veröffentlichen. Sie können sich bereits jetzt für diesen Kurs voranmelden. Wir benachrichtigen Sie, sobald ein Termin feststeht.
Umfang: 8 – 12 Lektionen
Schulstufe: ab dem 9. Schuljahr
Kursleitung: Dmitri Nikolenkov
Kurssprache: Deutsch oder Englisch, je nach Präferenz der Teilnehmenden
Veranstaltungsort: ETH Zürich, 8092 Zürich. Der genaue Veranstaltungsort wird paar Tage vor Kursbeginn bekanntgegeben, damit wir die Raumgrösse flexibel planen können.
Voranmeldung: externe Seitezum Voranmeldeformular
Sie können sich bis zu zwei Tage vor Kursbeginn anmelden. Melden Sie sich bei Schwierigkeiten unter bei uns.
Wir untersuchen mathematische strategische Spiele mit kompletter Information. Die Herausforderung ist, die optimale Strategie zu finden, die entweder zu einem Gewinn oder zum gewünschten Zustand innerhalb des Spiels führt. Allgemeine Strategien wie gewinnende Positionen, Symmetrie, Rückwärtsanalyse werden anhand der zugänglichen Beispiele erprobt und erklärt. Das Spielen (NIM, 9 Löcher, SET Game etc.) wird auch nicht zu kurz kommen.
Beispiel 1: NIM Spiel
Das NIM-Spiel ist ein Spiel für zwei Personen, bei dem abwechselnd eine Anzahl von Bonbons weggenommen wird. Gewonnen hat beim Standardspiel derjenige, der das letzte Bonbon nimmt. Es gibt viele verschiedene Versionen davon.
Version A: Ein Haufen mit 13 Bonbons. In einem Zug darf man 1 bis 3 Bonbons nehmen.
Version B: 3 Haufen mit 3, 4 und 5 Bonbons. In einem Zug darf man beliebig viele Bonbons aber nur aus einem Haufen nehmen.
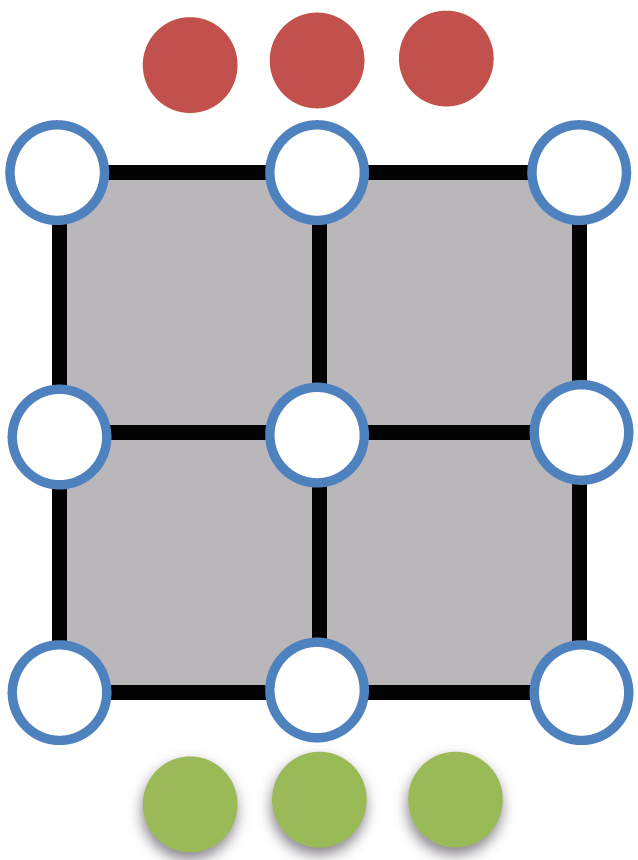
Beispiel 2: 9 Löcher Spiel
Eine Version vom gut bekannten Tic-Tak-Toe Spiel erlaubt das mathematische und strategische Denken zu fördern.
Das Spielfeld sieht aus wie ein 2x2 Quadrat mit Gitternetzlinien.
Jeder Spieler hat 3 Spielsteine, das Ziel ist drei eigene Steine in eine horizontale, vertikale oder diagonale Linie zu platzieren.
Zwei Spieler machen ihre Züge abwechslungsweise.
Zuerst setzen die Spieler ihre Steine in die Löcher, dann ziehen sie.
Version A: Nachdem die Spieler ihre Steine aufs Spielfeld gesetzt haben, dürfen sie in einem Zug ein freies Feld belegen („Springen erlaubt“).
Version B: Nachdem die Spieler ihre Steine aufs Spielfeld gesetzt haben, dürfen sie in einem Zug ihren Stein auf ein freies Feld ziehen, nur wenn es mit der Position des Steines durch eine Linie verbunden ist.
Nächster Termin: Wir werden in Kürze einen Termin veröffentlichen. Sie können sich bereits jetzt für diesen Kurs voranmelden. Wir benachrichtigen Sie, sobald ein Termin feststeht.
Umfang: 6 Treffen mit jeweils einer Doppellektion (12 Lektionen)
Schulstufe: ab dem 9. Schuljahr
Kursleitung: Lorenz Stäheli
Veranstaltungsort: ETH Zürich, 8092 Zürich. Der genaue Veranstaltungsort wird kurz vor Kursbeginn bekanntgegeben, damit wir die Raumgrösse flexibel planen können.
Voranmeldung: externe Seitezum Voranmeldeformular
Sie können sich bis zu zwei Tage vor Kursbeginn anmelden. Melden Sie sich bei Schwierigkeiten unter bei uns.
Wie packe ich am besten Matheprobleme an?
Manchmal ist der Mathematikunterricht geprägt von Routineaufgaben verschiedenen Typs. Erkennt man den Typ, so ist mehr oder weniger klar, wie der Lösungsweg gestaltet werden muss. Dagegen stellen sich in der Praxis sehr oft Probleme, bei denen überhaupt nicht klar ist, wie man sie anpacken soll. Da sind gute Ideen und Strategien gefragt, Versuche können scheitern, andere zu überraschend schönen Einsichten führen.
In diesem Kurs soll das Problemlösen selbst in den Fokus gerückt werden. Was für Strategien können helfen, bei einem offenen Problem auf einen vielversprechenden Lösungsweg zu kommen? Welche Methoden sind besonders typisch für die Mathematik und daher immer wieder anzutreffen, an der Hochschule noch mehr als am Gymnasium? Das Lernziel dieses Kurses besteht also darin, dass die Teilnehmer darin unterstützt werden, bei offenen Problemen erfolgversprechende Strategien zu wählen.
Wir werden zahlreiche attraktive Problemstellungen untersuchen und uns beim Lösen immer wieder selber über die Schulter schauen, um besonders erfolgversprechende Problemlösungsstrategien zu identifizieren. Die Aufgaben sind dabei so gehalten, dass nur geringe fachliche Vorkenntnisse nötig sind. Die Kenntnisse, die Sie beim Eintritt ins Kurzzeitgymnasium mitbringen, reichen völlig aus.
Wenn es Sie also reizt, sich spannenden Problemen zu stellen, zu knobeln, Wege auszuprobieren und zu verwerfen, und schöne Lösungen zu geniessen, und wenn es Sie gleichermassen reizt, dabei Strategien zu lernen, die Ihnen auch später immer wieder dienlich sein werden, dann sind Sie in diesem Kurs genau richtig.
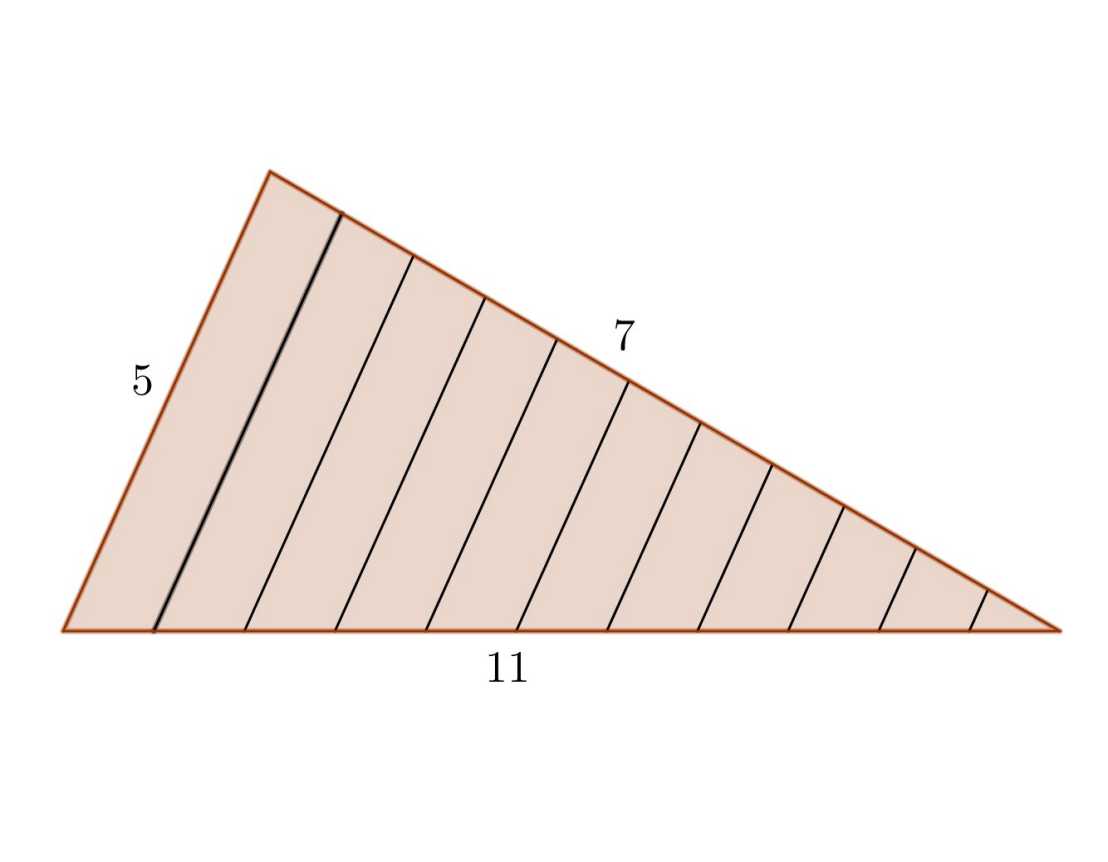
In dem abgebildeten Dreieck mit den Seitenlängen 11, 7 und 5 sind 10 Strecken eingezeichnet worden, die alle parallel zur kürzesten Dreiecksseite sind. Sie unterteilen das Dreieck in 11 gleich breite Streifen.
Wenn man die Längen all dieser 10 Strecken addiert, welche Summe erhält man dann?
Anna und Maria treffen sich in einem Café. Im Laufe des Gesprächs finden sie Folgendes über ihr Alter heraus.
Maria ist heute 24 Jahre alt. Sie ist doppelt so alt, wie Anna war, als Maria so alt war, wie Anna jetzt ist. Wie alt ist Anna heute?
Nächster Termin: Wir werden in Kürze einen Termin veröffentlichen. Sie können sich bereits jetzt für diesen Kurs voranmelden. Wir benachrichtigen Sie, sobald ein Termin feststeht.
Umfang: 6 Lektionen
Schulstufe: ab dem 10. Schuljahr
Kursleitung: Lorenz Stäheli
Veranstaltungsort: ETH Zürich, 8092 Zürich. Der genaue Veranstaltungsort wird kurz vor Kursbeginn bekanntgegeben, damit wir die Raumgrösse flexibel planen können.
Voranmeldung: externe Seitezum Voranmeldeformular
Sie können sich bis zu zwei Tage vor . Melden Sie sich bei Schwierigkeiten unter bei uns.
Was macht die Einschätzung von Wahrscheinlichkeiten so schwierig?
Drei Beispiele für gängige Irrtümer
Beispiel 1: Tochter oder Sohn?
Wenn ich Ihnen verrate, dass ich zwei Kinder habe und dass eines davon ein Mädchen ist. Wie gross würden Sie dann die Wahrscheinlichkeit schätzen, dass mein zweites Kind ein Junge ist?
Schätzen Sie die Wahrscheinlichkeit auf 50 %, weil das zweite Kind mit etwa derselben Chance ein Mädchen oder Junge ist? Weit gefehlt, die Wahrscheinlichkeit liegt bei etwa 2/3, wie Sie im Kurs zur Wahrscheinlichkeitsrechnung und beurteilenden Statistik erfahren können.
Beispiel 2: Das Linda-Problem
Linda ist 31 Jahre alt, Single, direkt, offen und sehr intelligent. Linda hat Philosophie studiert und war sehr aktiv als Studentin: Sie war in Studentenbewegungen tätig und hat an verschiedenen Demonstrationen mitgewirkt (gegen Diskriminierung, gegen Nuklearwaffen, …). Was ist Ihrer Meinung nach wahrscheinlicher?
• Linda ist heute Bankangestellte.
• Linda ist heute Bankangestellte und ist aktiv in der Frauenbewegung.
Wenn Sie die zweite Aussage ausgewählt haben, so liegen Sie leider falsch. Denn tatsächlich ist die erste Aussage wahrscheinlicher. Auch das werden wir Ihnen im Kurs zur Wahrscheinlichkeitsrechnung und beurteilenden Statistik erklären.
Beispiel 3: Münzwurf
Hugo wirft 6-mal eine Münze, wobei bei jedem Wurf nur Kopf (K) oder Zahl (Z) beobachtet werden kann. Welche Abfolge ist wahrscheinlicher?
• ZKZKKZ
• KKKKKK
Haben Sie die erste Serie gewählt? Das trifft leider nicht zu. Denn beide Serien haben die gleiche Wahrscheinlichkeit, wie Sie im Kurs zur Wahrscheinlichkeitsrechnung und beurteilenden Statistik erfahren können.
Ziele der Unterrichtseinheit
In vielen Bereichen sind wir mit Ungewissheiten konfrontiert: Ist das Medikament wirksam? Wie gefährlich ist Autofahren? Wie gross ist die Gefahr eines Erdbebens? Aber auch im täglichen Leben trifft man laufend Entscheidungen, deren Ausgang nicht mit Sicherheit vorhersagbar sind. Eigentlich sind die mit Sicherheit vorhersagbaren Vorgänge eher selten in der Realität und nur eine Idealvorstellung in den Wissenschaften, die Welt zu modellieren.
Wie kann uns in dieser Ungewissheit gerade die Mathematik weiterhelfen? Die Wahrscheinlichkeitsrechnung und beurteilende Statistik beschäftigt sich mit Situationen, bei denen mehrere Ausgänge möglich sind und gibt uns so mittels Wahrscheinlichkeitsaussagen einen gewissen Grad an Gewissheit zurück.
Diese Unterrichtseinheit behandelt die Basiselemente der Wahrscheinlichkeitslehre und zeigt an ausgewählten Beispielen, wie diese Ideen zur Schätzung auf Grundlage einer Stichprobe und zum Testen einer Hypothese verwendet werden können. Damit ist diese Unterrichtseinheiten eine ideale Ergänzung zur ebenfalls in der ETH Youth Academy angebotenen beschreibenden Statistik.
Inhaltsübersicht
Grundbegriffe der Wahrscheinlichkeitsrechnung: Wie lässt sich herausfinden, mit welcher Wahrscheinlichkeit Ereignisse auftreten?
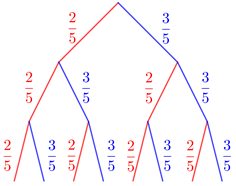
Baumdiagramme: Wie gewinne ich mit Baumdiagrammen eine Übersicht über die Wahrscheinlichkeit von Ereignissen?
Bedingte Wahrscheinlichkeit: Bei der bedingten Wahrscheinlichkeit gibt es einen statistischen Zusammenhang zwischen dem Eintreten von zwei Ereignissen, wie zum Beispiel zwischen dem Rauchen (Ereignis A) und dem Erkranken an Krebs (Ereignis B). Die bedingte Wahrscheinlichkeit kann also als Neueinschätzung der Wahrscheinlichkeit von Ereignis B interpretiert werden, wenn die Information vorliegt, dass Ereignis A bereits eingetreten ist. Wie lassen sich solche bedingten Wahrscheinlichkeiten berechnen?
Ein Beispiel für bedingte Wahrscheinlichkeit ist das sogenannte "Monty Hall Problem", zu dem Sie hier mehr dazu lesen können:
DownloadMonty Hall Problem (PDF, 83 KB)
Kombinatorik: Wie können wir mithilfe der Kombinatorik einen Überblick über die möglichen Ereignisse bekommen? Wie viele Möglichkeiten gibt es beispielsweise, mit zwei Würfeln die Augensumme 9 zu würfeln?
Zufallsgrössen und Verteilungen: Wahrscheinlichkeiten im Alltag
Wie viele Besucher waren auf der Jubiläumsfeier?
Ihr Gymnasium feiert an einem herrlichen Sommertag sein Jubiläum mit Ständen und Attraktionen draussen auf dem Schulhof. Zusammen mit ihrer Freundin haben Sie mit einer Drohne Bilder von dem Fest gemacht. Als Sie die Bilder betrachten, fragen Sie sich, wie viele Besucher wohl auf dem Fest gewesen sind.
Sie haben keine Lust, alle Personen auf dem Bild zu zählen. Daher wollen Sie eine Stichprobe nehmen und die Gesamtzahl abschätzen. Ihre Freundin zeichnet ein Raster mit hundert Felder über das Bild und schlägt vor, acht Felder auszuwerten.
Schätzen Sie die Besucherzahl:
Wählen Sie acht Felder aus und markieren Sie diese. Bestimmen Sie die Anzahl der Personen in diesen Feldern.
Schätzen Sie aus dieser Stichprobe die Gesamtzahl der Besucher ab.
Schätzen und Testen: Hypothesentests werden durchgeführt, wenn man mit erhobenen Daten etwas nachweisen möchte – zum Beispiel dass von bestimmten medizinischen Tests zehn Prozent falsch positiv sind. Um dies zu testen, muss also das Gegenteil widerlegt werden. Was bedeutet das für dieses Beispiel: Welche Behauptung muss in diesem Fall widerlegt werden?